Blenderでカーブの角度を計算するには？正規化・内積・アークコサインを使うとできる

Blenderのカーブ（ベジエ）を使用したジオメトリノードにおいて、「特定の角度のみオブジェクトを置きたい」「特定の角度以上の制御点だけ処理をしたい」なんて場面にでくわすかもしれません。そこで、ジオメトリノードで角度を算出するにはどうすればいいかを記載しています。なんか間違ってる可能性も大です。

テストを行うカーブ

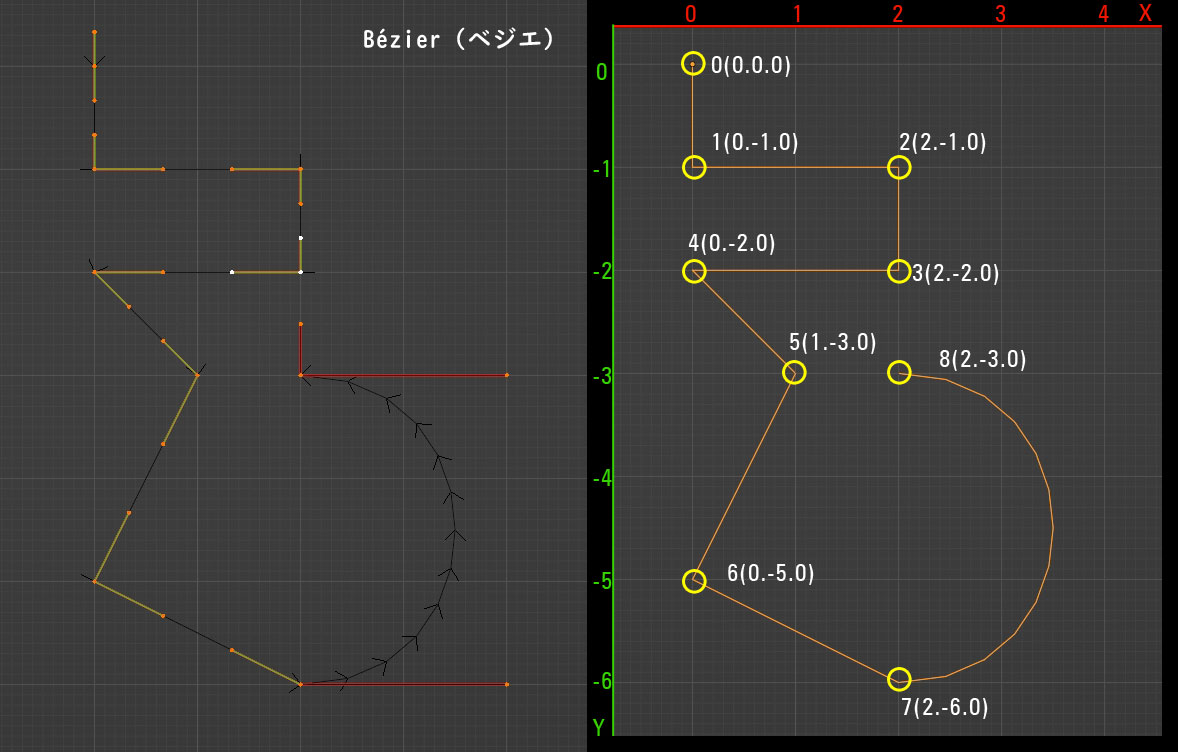
上図左のようなベジエを用意しました。直角や斜め、一部は弧を描いているカーブです。一番左上を原点にしています。各制御点の位置（position）は上図右のようになっています。

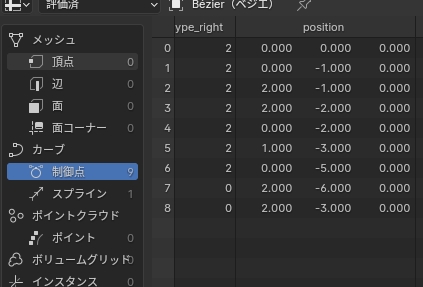
これらの座標はジオメトリノードの画面で表示されるスプレッドシートでも確認することができます。シーンのグローバル座標ではなく、オブジェクトの原点（この場合は左上の制御点）を基準にしたローカル座標になっているんですね。

角度を求めるには二つのベクトルが必要

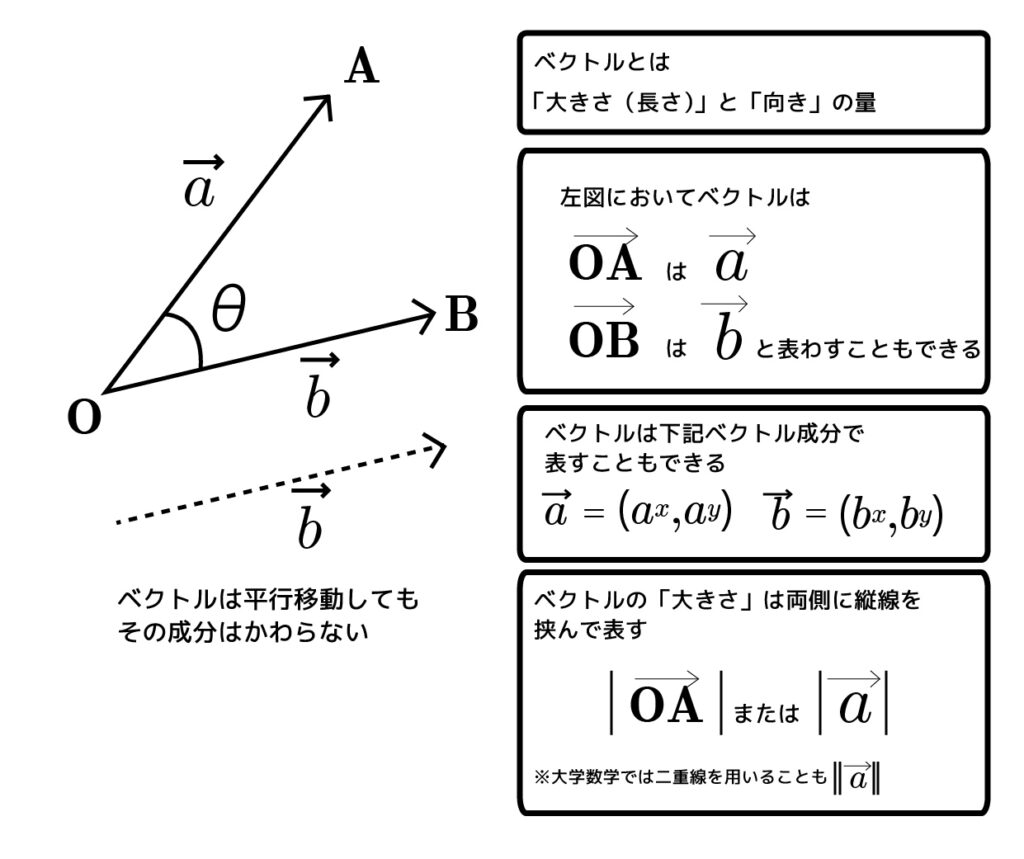
数学で習いましたね。忘れてますか？　私はすっかり忘れてます（全国偏差値70超えだったんですが…）。ベクトルとは大きさ（長さ）と向きの量であること、Oが始点になっていること、それぞれの記号は上図のとおりです。両側の縦線の意味を忘れており、調べる時に「ベクトル 縦の線 何」とあほみたいな検索をしてしまった。

まずはベクトルを求める

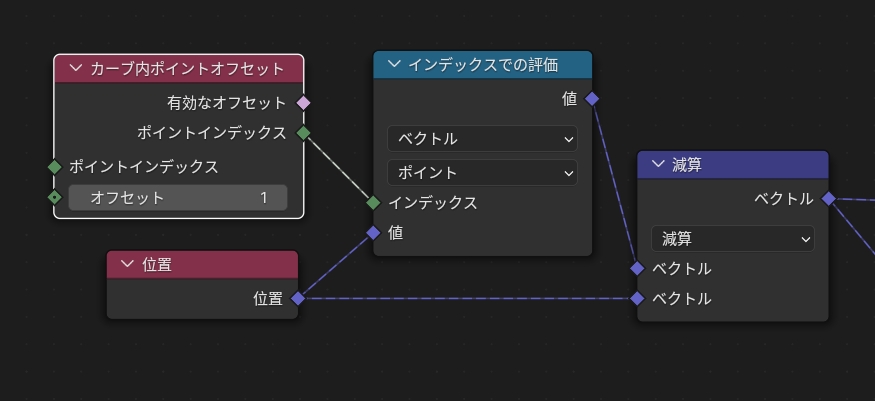
位置・カーブ内ポイントオフセット（Offset Point in Curve Node）・インデックスでの評価（Evaluate at Index Node）・減算（数式）ノードを使用します。インデックスでの評価（Evaluate at Index Node）は他の要素（今回の場合は制御点）にアクセスできる便利なノードです。カーブ内ポイントオフセット（Offset Point in Curve Node）を用いると、自分の制御点を基準にいくつ先（または前）の制御点かを指定できます。値はその制御点のどんな情報を取得したいかを設定するので、今回は位置ノードを繋ぎます。

自分の位置と次の位置

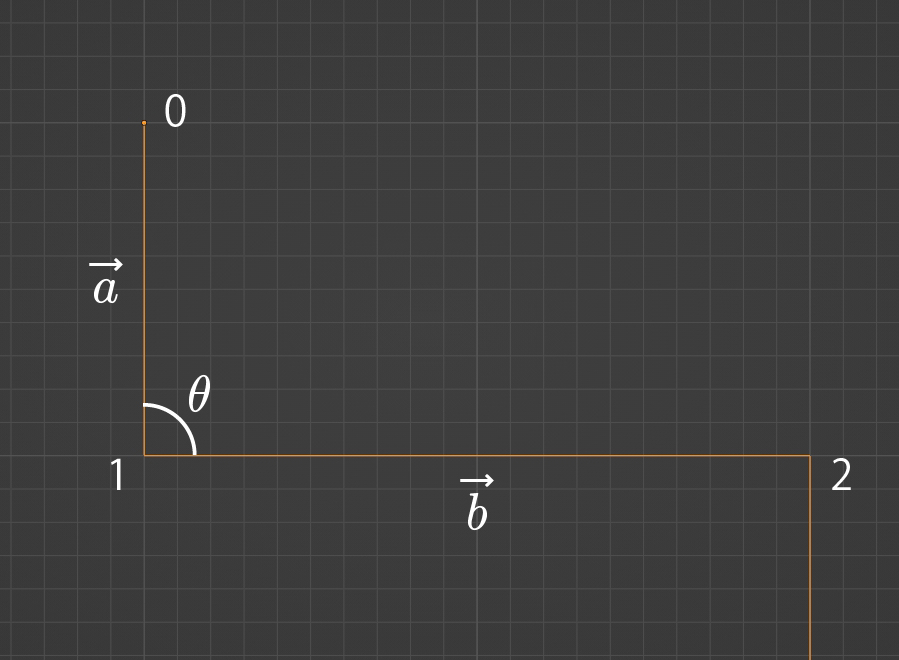
例えばインデックス番号1の位置座標（0,-1,0）を基準に考えてみます（0はそもそも角度がないので）。b→を求めるには、インデックス番号1と2の位置座標が必要ですね。

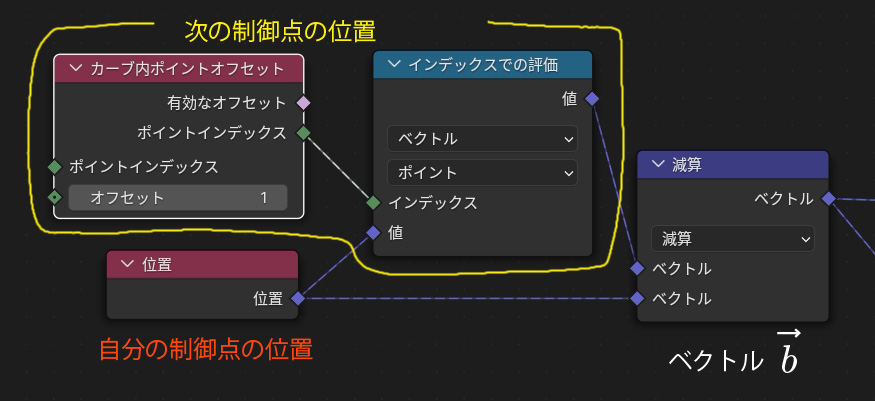
まず自分の位置を取得するために位置ノードを利用します。そして次の制御点を取得したいのでカーブ内ポイントオフセット（Offset Point in Curve Node）に「１」をオフセットに入力します。オフセットの名の通り相対なので、インデックス番号1の場合はインデックス番号2を指定することになります。これにより、インデックスでの評価（Evaluate at Index Node）ではインデックス番号2の(-2,-1,0）が取得できます。そしてこれらの差を計算ノードの減算を使って算出したものがb→になるわけです。注意点として、インデックス1を始点とした2へのベクトルであるということを理解しておく必要があります。

自分の位置と前の位置

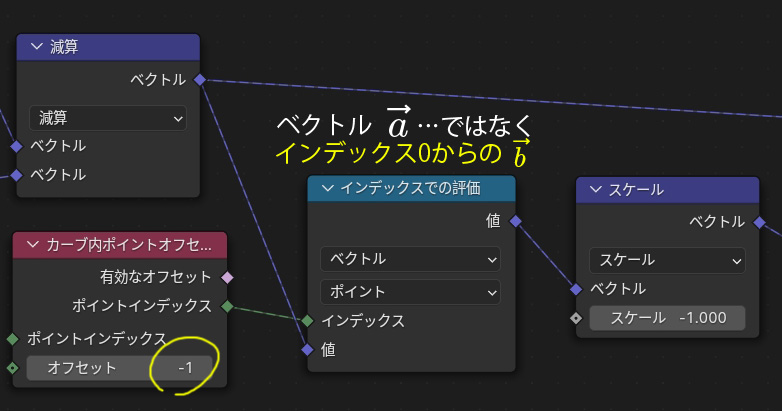
ベクトルa→を求めるためにはインデックス0の位置が必要なのですが、再度計算する必要はありません。上図のようなノードを組むと、一つ前のインデックス0を始点とした1へのベクトルが取得できます。ジオメトリノードはこういった情報の結果のつなぎ合わせが便利な半面、頭の中で理解しつつ組まないと訳がわからくなります（なんとかしてほしい）。これで一応はベクトルa→が取得できるのですが、厳密にはインデックス0を始点とした1へのベクトルb→であることがわかりますでしょうか。つまり向きが違うのです。

そのために登場するのがスケール（ベクトル演算）ノードです。要はベクトルの向きを逆にしてしまえば、a→と一緒になるということなんですね。始点は0のままなんですが、ベクトルは平行移動しても成分は変わないので同一と扱うことができます。

内積とアークコサイン

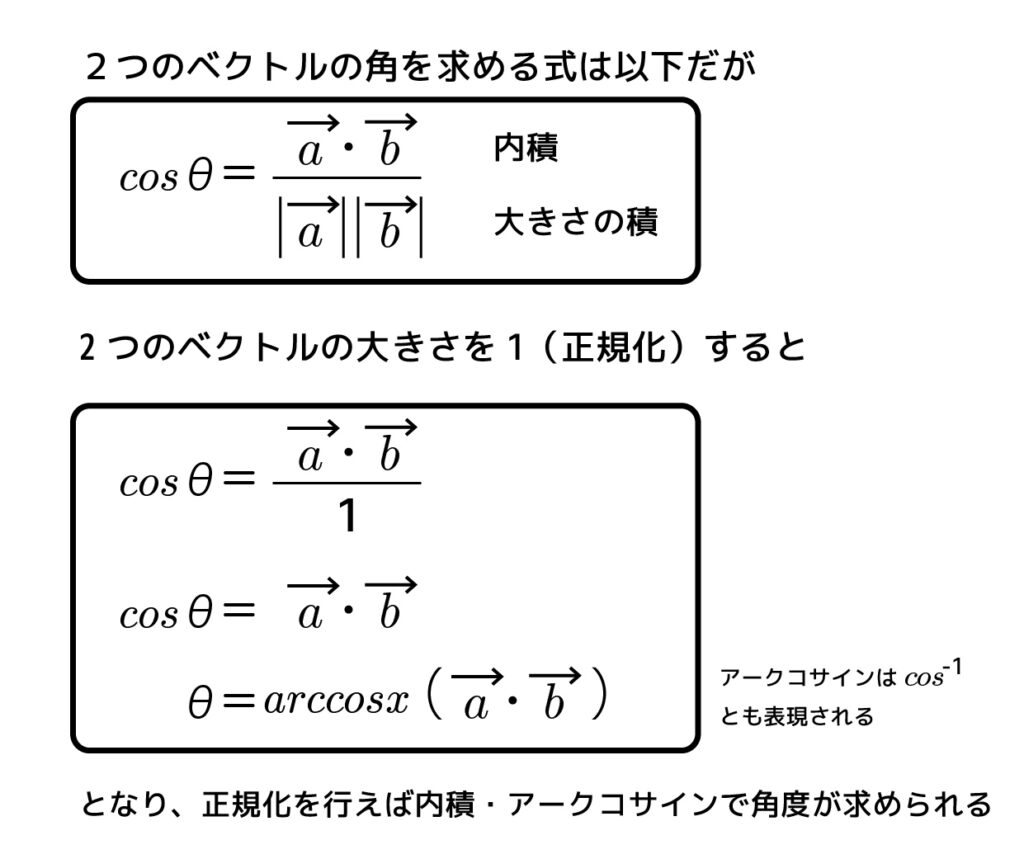
ここからは数学の基礎知識が必要なのですが、他のサイトで見かける数式や内積、コサインを用いた角度の計算式ではなく、Blender上でどうやって計算するかに焦点を当てます。他のブログ記事「ゲームエンジンで理解する内積」がめちゃくちゃ参考になるので計算過程や理論はそちらにおまかせして、簡単にまとめると上記のような求めかたになります。正規化・内積・アークコサインの順でノードを繋げば角度が出てくるんですね。

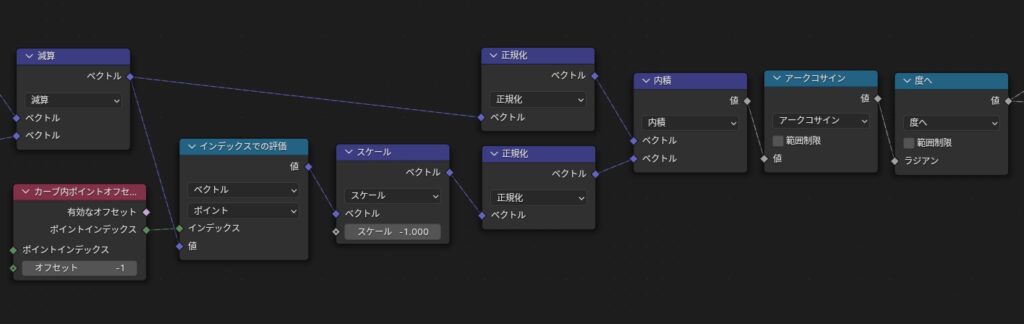
a→とb→をベクトル演算ノードで正規化し、同ノードで内積を求めてアークコサイン（数式ノード）に渡します。出力される値はラジアンになるので、度へ（数式ノード）で角度に変換します。

結果

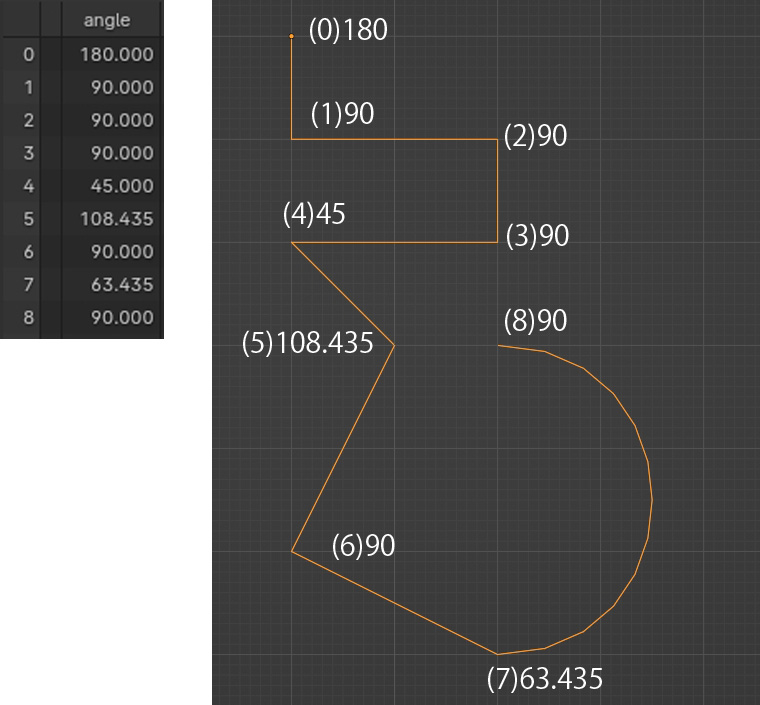
概ね想定通りのカーブが算出されました。最初と最後の制御点は前後の点が無いため角度としてはおかしいのですが、ジオメトリノードには端を選択というノードもあるため制御はできそうです。7番の角度がおかしいと思われそうですが、この計算はあくまでも7から8への制御点を直線で結んだ際の角度なのでこれであっています。

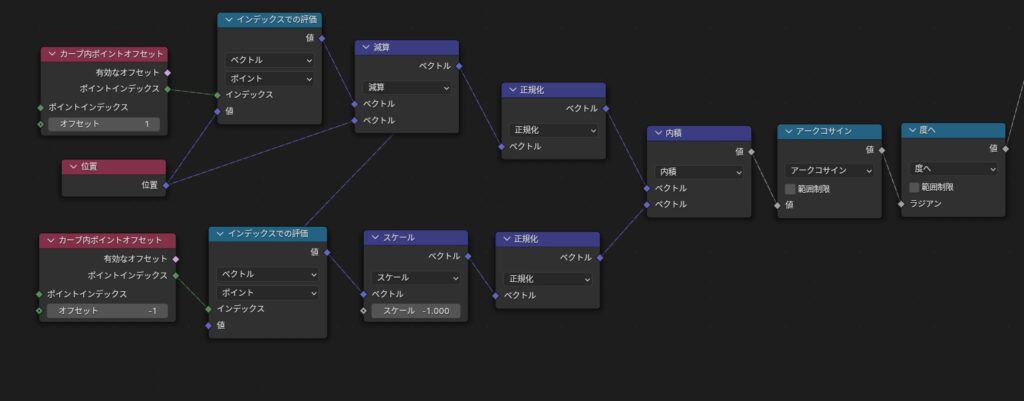
あらためて全体のノードです。意外にシンプルですね。

正規化（Normalize）とは

今回の処理においての正規化とは、長さを1に調整する意味になります。他で例えると「単価」みたいなものでしょうか。10個で千円の商品があった場合、1個は何円？を求めるようなイメージです。この正規化したベクトルを「単位ベクトル」とも呼称します。ベクトルは大きさと向きで構成されているので、向きは違っても大きさの単位を揃えておくと計算上なにかと便利になる…という理屈です。細かいことは私もわかりません。

ということでカーブの角度を求めるジオメトリノードの計算式でしたが、他のノードでカーブの制御点を選択したい場合はこちらの「【ジオメトリノードの選択を使いこなす】任意の点にオブジェクト出し分ける方法（カーブ編）」を御覧ください。

                   

備忘録として残しておきます。